[LeetCode] 22. Generate Parentheses

Table of Contents

Description

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Example 2:

Input: n = 1
Output: ["()"]

Constraints:

• $1 <= n <= 8$

Approach - 1

Use recursion to generate valid parentheses combinations. Starting with the base case of a single pair (), it builds larger solutions by inserting a new pair into all possible positions of smaller combinations. To ensure uniqueness, insertion stops when encountering a closing parenthesis, avoiding duplicates.

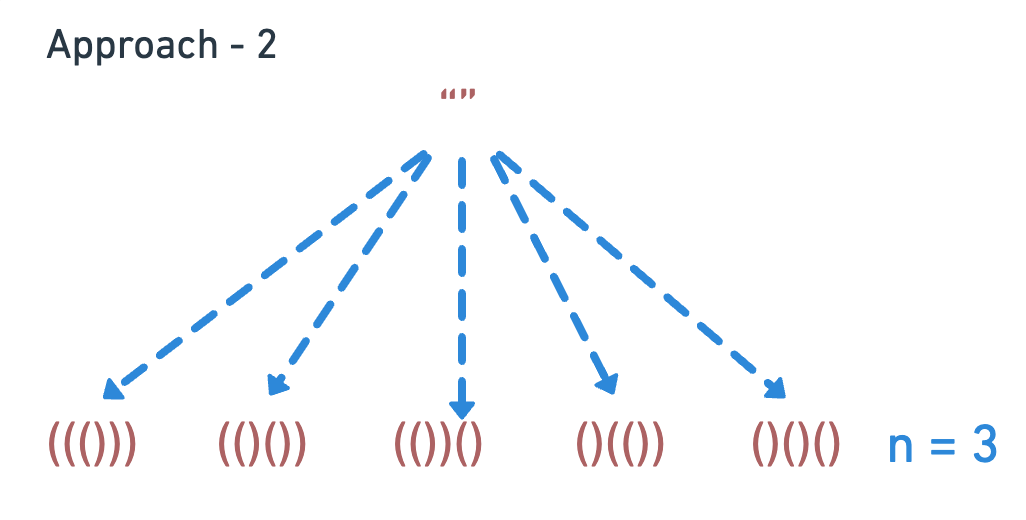
Approach - 2

Uses a recursive function with parameters to track the current string, the count of open parentheses, and the count of close parentheses. It builds valid combinations by adding an open parenthesis if possible and a close parenthesis if it doesn’t exceed the number of open parentheses.The difference with Approach - 1 is that it doesn’t rely on string slicing to insert parentheses.

Solution - 1

const OPEN_PARENTHESIS = "(";
const CLOSE_PARENTHESIS = ")";

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function (n) {
  // Base case: For 1 pair, the only valid combination is "()".
  if (n === 1) return [`${OPEN_PARENTHESIS}${CLOSE_PARENTHESIS}`];

  // Recursively generate the combinations for n-1 pairs.
  return generateParenthesis(n - 1).flatMap(parentheses => {
    let result = [];

    // Loop through each index in the current combination.
    for (let i = 0; i < parentheses.length; i++) {
      // Create a new parentheses by inserting "()" into the current combination.
      result.push(
        `${parentheses.slice(0, i)}${OPEN_PARENTHESIS}${CLOSE_PARENTHESIS}${parentheses.slice(i)}`
      );
      // If the current character is an closing parenthesis,
      // break out of the loop. This avoids generating duplicate combinations.
      if (parentheses[i] === CLOSE_PARENTHESIS) break;
    }

    return result;
  });
};

Solution - 2

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function (
  n,
  str = "",
  openParenthesisCount = 0,
  closeParenthesisCount = 0
) {
  // Base condition: reached maximum length; return current combination.
  if (str.length === n * 2) return [str];

  let result = [];

  // If we can add an open parenthesis, add it and continue recursion.
  if (openParenthesisCount < n)
    result = result.concat(
      generateParenthesis(
        n,
        `${str}${OPEN_PARENTHESIS}`,
        openParenthesisCount + 1,
        closeParenthesisCount
      )
    );

  // If it's valid to add a close parenthesis, add it.
  if (closeParenthesisCount < openParenthesisCount)
    result = result.concat(
      generateParenthesis(
        n,
        `${str}${CLOSE_PARENTHESIS}`,
        openParenthesisCount,
        closeParenthesisCount + 1
      )
    );

  return result;
};

Complexity Analysis

Time Complexity

The time complexity is determined by the number of valid combinations of parentheses. The number of valid combinations for n pairs of parentheses is given by the $n$-th Catalan number, which is approximately $O(\frac{4^n}{n^{3/2}})$. And we also need to consider the time taken to generate each combination, which is $O(n)$ for each combination. Therefore, the overall time complexity is $O(\frac{4^n}{n^{3/2}} \cdot n) = O(\frac{4^n}{n^{1/2}})$.

Space Complexity

The space complexity is $O(n)$ for the recursion stack and the space used to store the result. The recursion stack can go up to a depth of n, and the result array will store all valid combinations, which can be up to $O(\frac{4^n}{n^{3/2}})$ in size. Therefore, the overall space complexity is $O(\frac{4^n}{n^{3/2}} + n) = O(\frac{4^n}{n^{3/2}})$.